Seven AI Workers

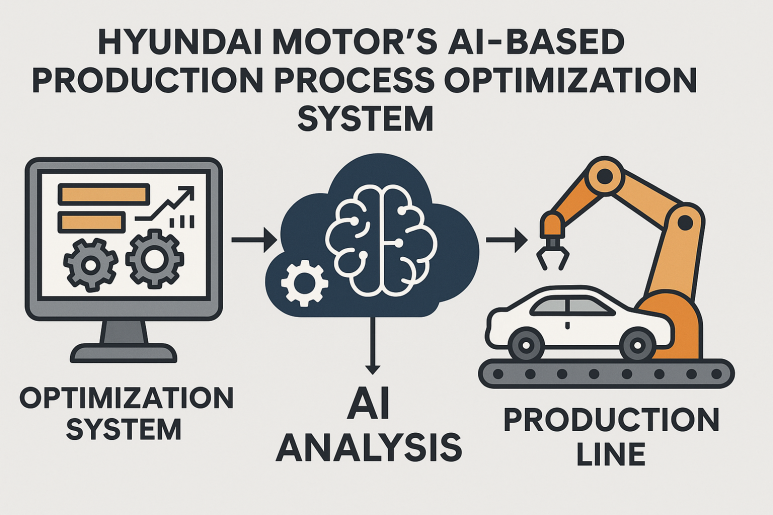
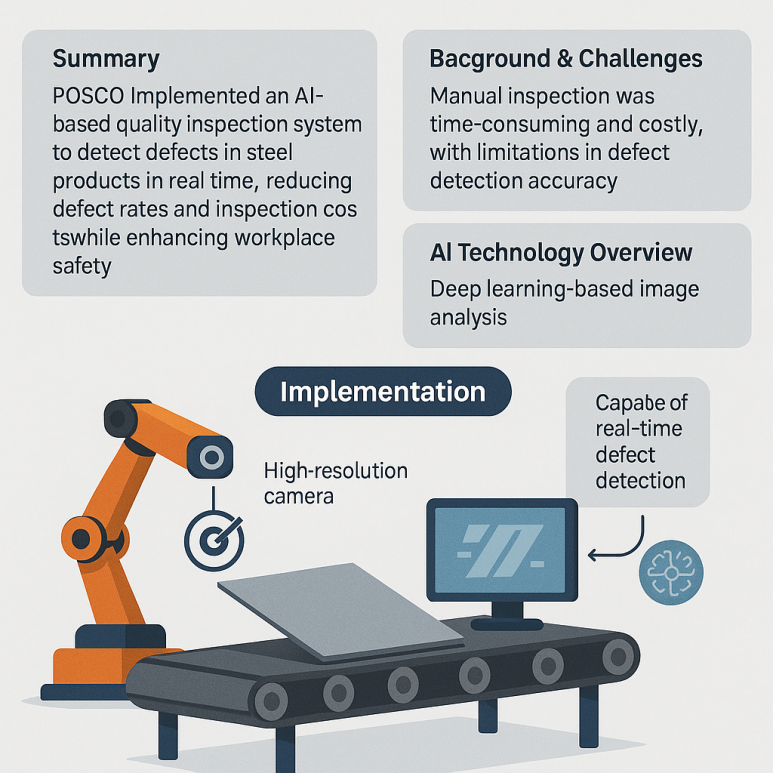
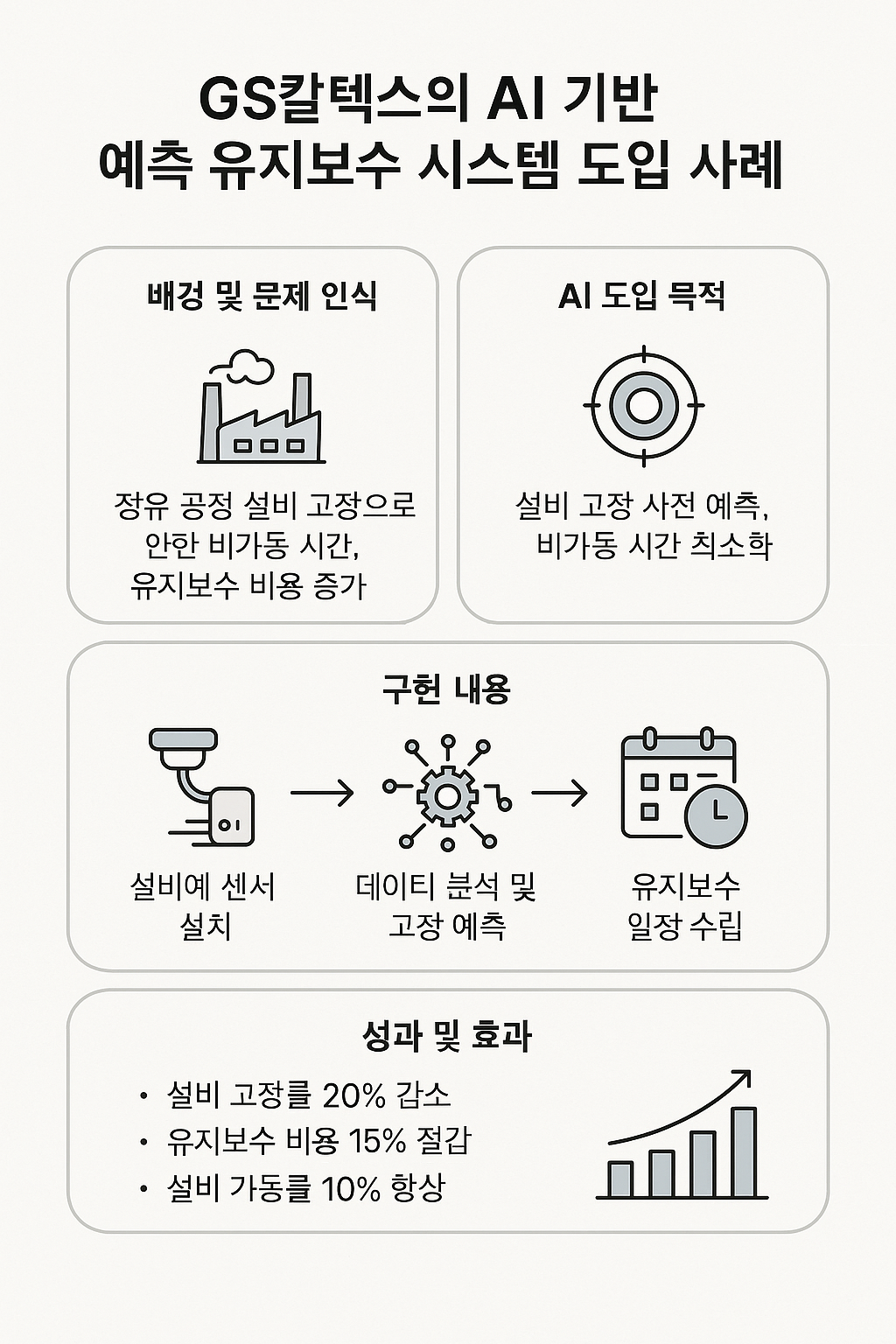
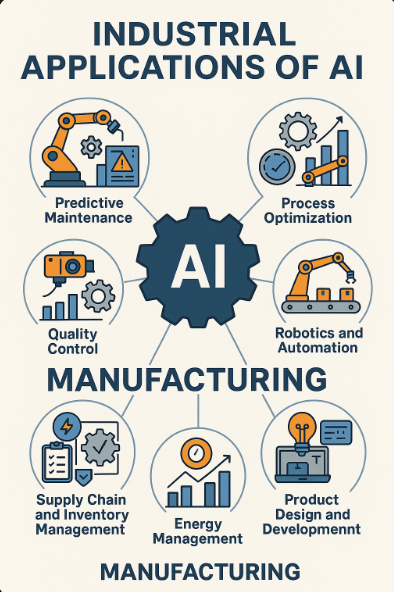
제조업에서 인공지능(AI)을 활용한 생산 공정 최적화(Process Optimization)는 효율성 향상, 비용 절감, 품질 개선 등 다양한 성과를 창출하고 있습니다. 아래는 국내외 제조업체들의 AI 기반 생산 공정 최적화 사례를 정리한 내용입니다.​1. 인공지능 활용 공정 최적화 (Process Optimization) ​도입 목적생산 공정의 병목 현상 해소자원 배분의 최적화생산 속도 및 품질 향상​기술 개요활용한 AI 기술: 머신러닝 기반의 공정 최적화 알고리즘주요 기술적 특징 및 선정 이유: 실시간 데이터 분석을 통해 공정의 이상 징후를 조기에 감지하고, 자원 배분을 최적화할 수 있는 능력 때문입니다.구현 내용시스템 구조 또는 도입 모델 개요:생산 라인에서 실시간 데이터 수집AI 모델을 통한 데이..

제조업에서 주요 기업은 자사의 특성과 필요에 맞춰 인공지능(AI)을 활용한 품질 검사 및 결함 탐지 시스템을 도입하여 경쟁력을 강화하고 있습니다.​1. 인공지능 기반 품질 검사 및 결함 탐지 시스템 (Quality Control and Defect Detection)​AI 기반 품질 검사 및 결함 탐지 시스템 도입 목적품질 검사/결함 감지 정확도 향상검사 시간 단축 및 비용 절감불량률 감소 및 재작업 비용 절감생산 효율성 향상작업 현장의 안전성 강화​도입 기술 개요활용한 AI 기술: 딥러닝 기반의 이미지 분석 기술주요 기술적 특징 및 선정 이유: 대량의 이미지 데이터를 학습하여 결함을 자동으로 감지하고, 실시간으로 분석할 수 있는 능력 때문입니다.​구현 내용시스템 구조 또는 도입 모델 개요:생산 라인에 ..

제조업에서 인공지능(AI)을 활용한 예측 유지보수(Predictive Maintenance)는 설비 고장을 사전에 예측하여 생산 효율성을 높이고 유지보수 비용을 절감하는 데 중요한 역할을 합니다. 아래는 국내외 제조업체들의 AI 기반 예측 유지보수 사례를 정리한 내용입니다. 1. 인공지능 기반 예측 유지보수 시스템AI 기반 예측 유지보수 시스템 도입 목적설비 고장을 사전에 예측하여 비가동 시간 최소화유지보수 비용 절감 및 설비 수명 연장작업자 안전 강화도입 기술 개요활용한 AI 기술: 딥러닝 기반의 예측 모델주요 기술적 특징 및 선정 이유: 설비에서 수집된 센서 데이터를 분석하여 고장 징후를 사전에 감지하고, 유지보수 시점을 예측하는 데 효과적이기 때문입니다.구현 내용시스템 구조 또는 도입 모델 개요:설..

1. 예측 유지보수 (Predictive Maintenance)적용 배경 및 목적: 설비 고장을 사전에 예측하여 비가동 시간을 최소화하고 유지보수 비용을 절감하기 위함입니다.해외 사례 – Siemens: Siemens는 AI 기반의 예지보전 시스템을 도입하여 설비의 상태를 실시간으로 모니터링하고, 고장 가능성을 예측하여 유지보수 일정을 최적화하였습니다.국내 사례 – GS칼텍스: GS칼텍스는 AI 기반 가상 센서를 도입하여 원유 정제 과정에서 코크 함량을 예측하고, 이를 통해 설비의 이상 징후를 조기에 감지하여 유지보수 시기를 최적화하였습니다. 2. 품질 검사 및 결함 탐지 (Quality Control and Defect Detection)적용 배경 및 목적: 제품의 품질을 향상시키고 불량률을 감소시키기..

✅ 최적해란 무엇인가요?최적화 문제에서는 특정 목표를 달성하기 위해 변수들을 조정합니다. 이때 가장 좋은 결과를 주는 변수들의 조합을 '최적해'라고 합니다.최적해(Optimal Solution): 목표 함수를 최대화하거나 최소화하는 변수들의 조합입니다.전역 최적해(Global Optimum): 모든 가능한 해 중에서 가장 좋은 해입니다.지역 최적해(Local Optimum): 일정 범위 내에서 가장 좋은 해지만, 전체 범위에서는 아닐 수 있습니다.🧩 볼록성(Convexity)이란?볼록성은 최적화 문제를 훨씬 쉽게 풀 수 있도록 도와주는 성질입니다. "볼록다(Convex)"는 것은 데이터 구조가 하나의 점을 더 이상 최적해 통하지 않고 오류에 걸려 서로 밀어지는 것을 말하며, 전형적인 최적해를 검색할 때..

최적화(Optimization)는 어떤 문제에서 가장 "좋은" 해를 찾는 수학적 과정입니다. 이 과정은 크게 세 가지 기본 구성 요소로 이루어집니다:1. 의사결정 변수 (Decision Variables)의사결정 변수는 우리가 조정하거나 선택할 수 있는 변수입니다. 문제를 해결하기 위해 어떤 값을 "결정"해야 하는 대상입니다. 예를 들어:공장 생산 계획 문제에서: 각 제품을 몇 개 생산할 것인가?회귀 분석에서: 회귀 계수를 어떤 값으로 설정할 것인가?인공지능 모델 학습에서: 가중치 파라미터를 어떤 값으로 설정할 것인가?의사결정 변수는 일반적으로 x, y, w, θ 등의 기호로 표현되며, 최적화 문제에서는 이 변수들의 값을 결정하는 것이 목표입니다.2. 목적 함수 (Objective Function)목적 ..

3. 머신러닝과 AI에서의 최적화 활용 🤖최적화는 머신러닝과 인공지능(AI) 전반에 걸쳐 핵심적인 역할을 합니다. 복잡한 문제를 수학적으로 모델링하고 해결하는 과정에서 다양한 최적화 기법이 사용됩니다. 여기에서는 대표적인 세 가지 영역 — 딥러닝 학습, 하이퍼파라미터 튜닝, 강화학습(RL) — 에서 최적화가 어떻게 활용되는지 살펴봅니다.3.1 딥러닝 학습에서의 최적화 🧠딥러닝은 수백만 개의 파라미터를 가진 신경망을 학습시키는 과정입니다. 이 과정은 다음과 같은 최적화 문제로 표현됩니다:목표 함수: 손실 함수 (예: 교차 엔트로피, MSE)최적화 변수: 가중치, 편향 등 신경망의 파라미터제약 조건: 일반적으로 없음 (하지만 정규화 기법은 간접적인 제약을 추가)이 손실 함수를 최소화하는 것이 학습의 본질..

1. 최적화란 무엇인가? 🤔최적화(Optimization)란 주어진 제약 조건 하에서 어떤 문제에 대해 ‘가장 좋은(best)’ 해답을 찾는 수학적 기법입니다.공식적으로는 의사결정 변수(우리가 조정할 수 있는 수치), 목적 함수(최대화 혹은 최소화하고자 하는 성능 지표), 그리고 제약 조건(허용 가능한 해를 제한하는 조건)으로 구성됩니다.예를 들어, 딥러닝 모델의 학습은 손실 함수를 최소화하는 비선형 최적화 문제이며, 생산 공정의 수익을 자원 제약 하에 최대화하는 문제는 선형 계획법 문제로 볼 수 있습니다.1.1 최적해와 볼록성 🔍전역 최적해(Global Optimum): 전체 가능한 해 중 목적 함수를 최적으로 만족하는 해지역 최적해(Local Optimum): 주변의 해보다 좋지만 전체 중에서는 ..

선형대수(Linear Algebra)는 벡터(vector), 행렬(matrix), 선형 변환(linear transformation)을 다루는 수학 분야로, 다차원 데이터를 표현하고 다루는 데 꼭 필요한 도구입니다. 인공지능(AI)에서는 이미지, 문장, 센서값 등 다양한 정보를 수치 벡터로 표현하고 이를 효율적으로 처리하기 위해 선형대수 지식이 필수입니다. 이 글에서는 선형대수의 핵심 개념들을 직관적으로 설명하고, 그것이 AI 시스템에서 어떻게 활용되는지 구체적인 예시와 함께 살펴보겠습니다.📌 1. 벡터와 벡터 공간(Vector & Vector Space)벡터는 크기와 방향을 가진 수학적 객체입니다. 예를 들어, 2차원 벡터 v= [x, y]는 가로(x)와 세로(y) 방향의 이동량을 나타내며, 공간 상..

인공지능(AI)은 불확실한 상황에서의 의사결정을 자주 요구받습니다. 이럴 때 확률 이론은 불확실성을 정량화하고 관리할 수 있는 수학적 틀을 제공하며, 통계학은 데이터를 기반으로 패턴을 추론하고 모델의 매개변수를 학습하는 도구입니다. AI 시스템이 불완전하거나 잡음이 많은 정보 속에서도 합리적인 판단을 내릴 수 있게 해주는 토대가 바로 이 두 가지입니다.확률에는 두 가지 주요 해석 방식이 있습니다: 빈도주의(frequentist)와 베이지안(Bayesian)입니다. 빈도주의는 반복된 시행에서 특정 사건이 일어날 비율로 확률을 정의합니다(예: 동전을 무수히 던졌을 때 앞면이 나올 확률은 0.5). 반면, 베이지안 해석은 확률을 신념의 정도로 보고, 새로운 정보가 들어올 때 기존 신념(사전 확률)을 갱신합니다..