728x90
✅ 최적해란 무엇인가요?
최적화 문제에서는 특정 목표를 달성하기 위해 변수들을 조정합니다. 이때 가장 좋은 결과를 주는 변수들의 조합을 '최적해'라고 합니다.
- 최적해(Optimal Solution): 목표 함수를 최대화하거나 최소화하는 변수들의 조합입니다.
- 전역 최적해(Global Optimum): 모든 가능한 해 중에서 가장 좋은 해입니다.
- 지역 최적해(Local Optimum): 일정 범위 내에서 가장 좋은 해지만, 전체 범위에서는 아닐 수 있습니다.
🧩 볼록성(Convexity)이란?
볼록성은 최적화 문제를 훨씬 쉽게 풀 수 있도록 도와주는 성질입니다. "볼록다(Convex)"는 것은 데이터 구조가 하나의 점을 더 이상 최적해 통하지 않고 오류에 걸려 서로 밀어지는 것을 말하며, 전형적인 최적해를 검색할 때 강력한 가능성을 제공합니다.
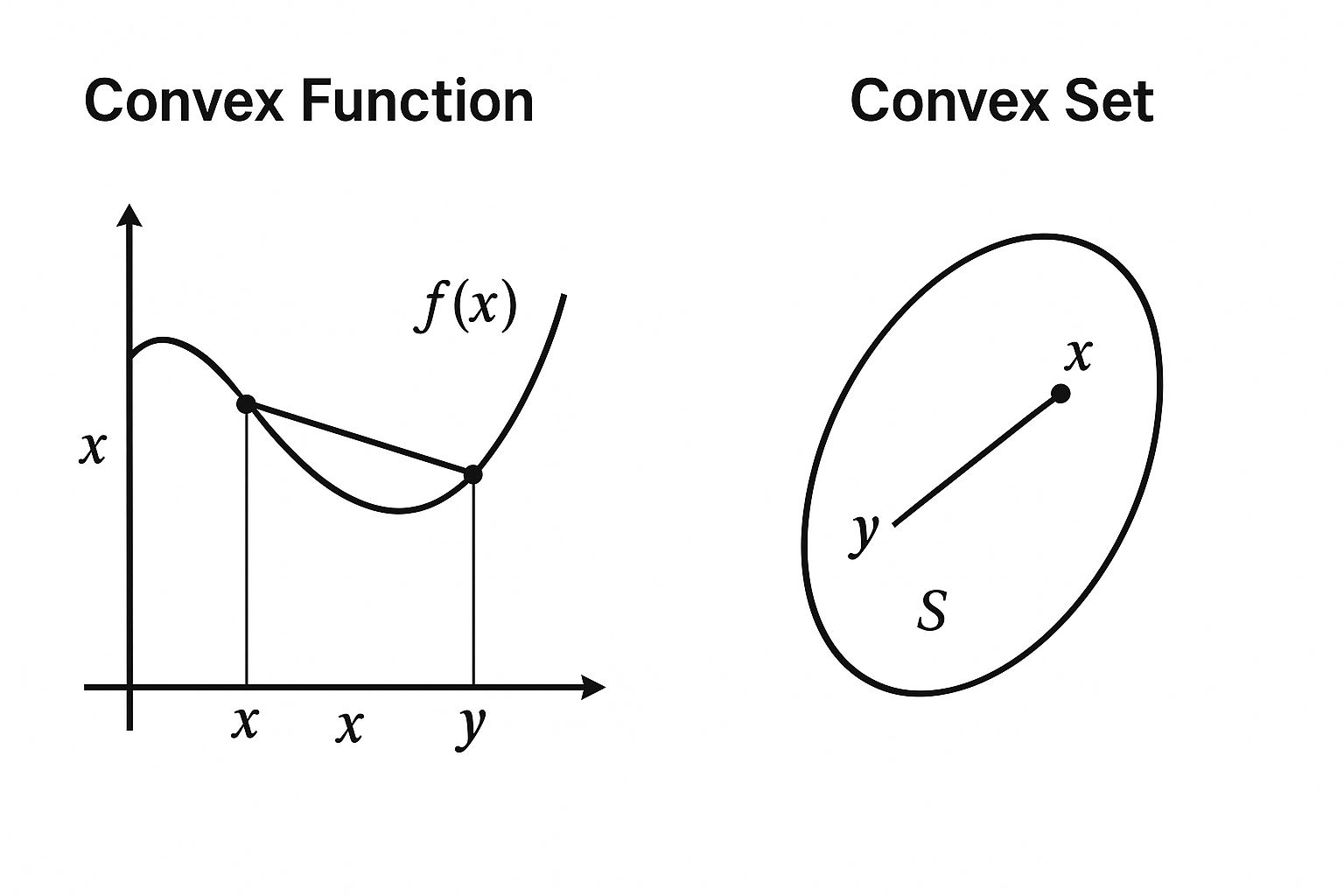
볼록 함수 (Convex Function)
- 함수가 아래로 볼록한 형태이면, 그래프 위의 어느 두 점을 직선으로 이었을 때, 그 직선이 항상 함수 그래프 위에 존재합니다.
- 이런 함수는 하나의 전역 최적해(Global Optimum)만 존재하게 되어, 로컬 최적해(Local Optima) 문제에서 자유롭습니다.
볼록 집합 (Convex Set)
- 제약 조건을 만족하는 해들의 모임(즉, 가능한 해의 집합)이 볼록하다면, 두 점을 연결한 직선 상의 모든 점도 유효한 해입니다.
- 이 역시 최적해를 찾는 데 유리한 구조를 제공합니다.
📊 왜 볼록성이 중요한가요?
볼록성은 최적화 문제를 해결하는 데 있어 다음과 같은 이점을 제공합니다:
- 해의 보장: 볼록한 문제에서는 지역 최적해가 전역 최적해이므로, 해를 찾는 것이 더 확실합니다.
- 효율성: 볼록한 문제는 알고리즘이 빠르게 수렴하여 해를 찾을 수 있습니다.
- 안정성: 해의 존재와 유일성이 보장되어, 결과에 대한 신뢰성이 높습니다.
🧠 예시로 이해하기
볼록성과 최적해의 개념을 이해하기 위해 다음과 같은 예시를 생각해볼 수 있습니다:
- 볼록한 경우: 산의 형태가 그릇처럼 오목한 경우, 공은 자연스럽게 가장 낮은 지점으로 굴러가며, 이 지점이 전역 최적해입니다.
- 비볼록한 경우: 산의 형태가 여러 개의 봉우리와 골짜기로 이루어진 경우, 공은 가장 낮은 지점이 아닌 중간의 골짜기에 멈출 수 있으며, 이는 지역 최적해입니다.
🔖 요약
- 최적해: 목표 함수를 가장 잘 만족시키는 변수들의 조합입니다.
- 볼록성: 문제의 구조가 볼록할수록 해를 찾기가 쉽고, 지역 최적해가 전역 최적해가 됩니다.
- 중요성: 볼록성은 최적화 문제의 해결 가능성과 효율성을 높여줍니다.
728x90
'인공지능 기본개념 및 용어' 카테고리의 다른 글
| 3.2.2 머신러닝 모델 학습과 평가 - Part1. 개요 (1) | 2025.05.26 |
|---|---|
| 3.2.1 머신러닝의 네 가지 주요 유형 이해하기 (4) | 2025.05.25 |
| 최적화 문제의 구성요소 3가지: 의사결정 변수, 목적 함수, 제약 조건 (0) | 2025.05.13 |
| 3.1.5 최적화(Optimization) Part.2 AI에서의 최적화 활용 (1) | 2025.05.13 |
| 3.1.5 최적화(Optimization) Part.1 개념 및 핵심기법 (0) | 2025.05.13 |