3.1.5 최적화(Optimization) Part.1 개념 및 핵심기법
1. 최적화란 무엇인가? 🤔
최적화(Optimization)란 주어진 제약 조건 하에서 어떤 문제에 대해 ‘가장 좋은(best)’ 해답을 찾는 수학적 기법입니다.
공식적으로는 의사결정 변수(우리가 조정할 수 있는 수치), 목적 함수(최대화 혹은 최소화하고자 하는 성능 지표), 그리고 제약 조건(허용 가능한 해를 제한하는 조건)으로 구성됩니다.
예를 들어, 딥러닝 모델의 학습은 손실 함수를 최소화하는 비선형 최적화 문제이며, 생산 공정의 수익을 자원 제약 하에 최대화하는 문제는 선형 계획법 문제로 볼 수 있습니다.
1.1 최적해와 볼록성 🔍
- 전역 최적해(Global Optimum): 전체 가능한 해 중 목적 함수를 최적으로 만족하는 해
- 지역 최적해(Local Optimum): 주변의 해보다 좋지만 전체 중에서는 아닐 수 있음
볼록성(Convexity)은 최적화 이론에서 핵심 개념입니다. 목적 함수와 제약 조건이 볼록(convex) 하면, 지역 최적해는 곧 전역 최적해가 됩니다. 이는 효율적인 알고리즘이 전역 해를 보장할 수 있게 해줍니다.
- 볼록 최적화 문제: 선형 회귀, 선형 계획법 등
- 비볼록 최적화 문제: 딥러닝 학습, 조합 최적화 등 – 해 찾기 어려움, NP-hard
🧭 다이어그램: 볼록 함수와 비볼록 함수 그래프 비교 (전역 최솟값 위치 시각화)
최적해와 볼록성 (Optimality and Convexity) (상세)
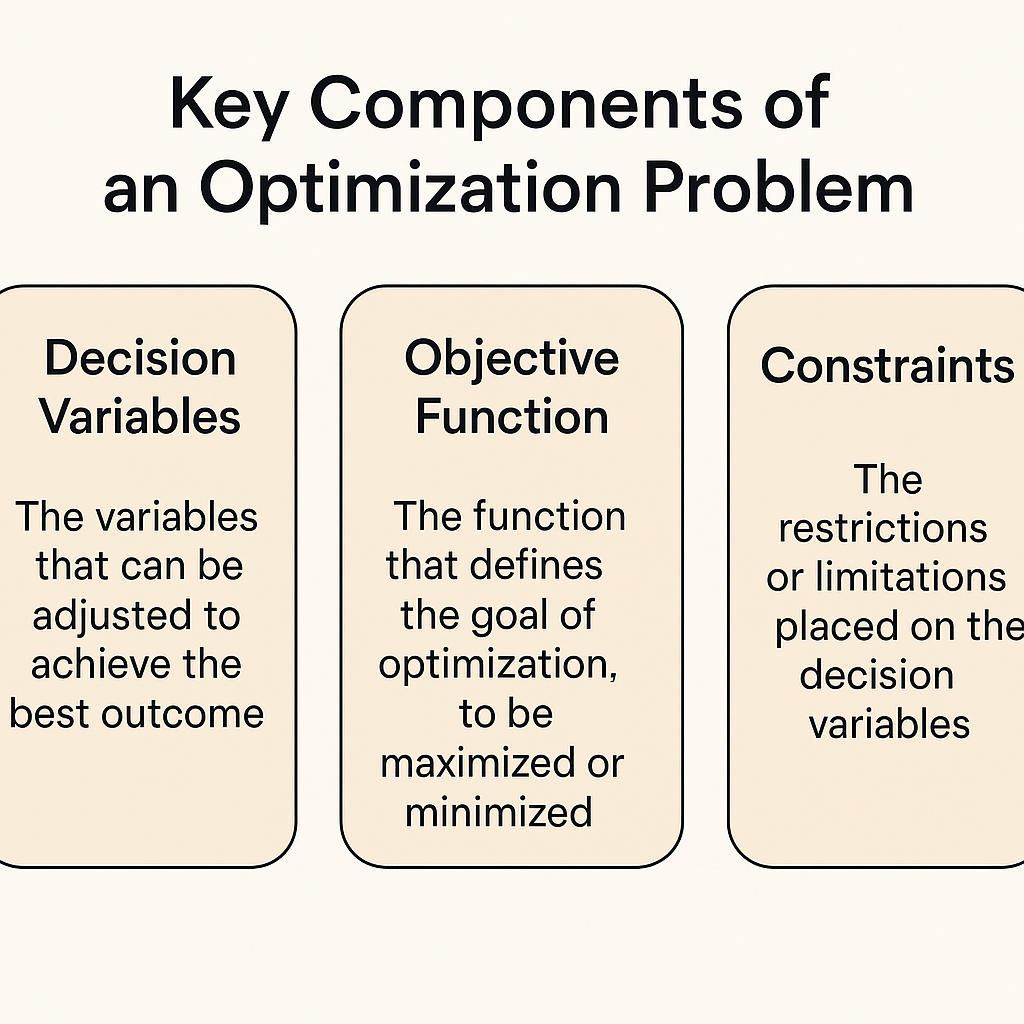
1.2 최적화 문제의 구성요소 🧩
- 의사결정 변수(Decision Variables): 조정 가능한 변수들
- 목적 함수(Objective Function): 최대/최소화하고자 하는 값 (예: 비용, 정확도)
- 제약 조건(Constraints): 변수에 대한 조건 (예: 자원, 예산)
이 요소들로 정의된 실현 가능 영역(feasible region) 내에서 최적 해를 찾는 것이 목표입니다. 경우에 따라 ‘충분히 좋은 근사 해’를 시간 내에 찾는 것도 현실적 해결법입니다.
최적화 문제의 구성요소 : 의사결정 변수, 목적 함수, 제약 조건 (상세)
2. 핵심 최적화 기법 🔧
2.1 선형 계획법 (Linear Programming, LP) 📊
선형 계획법은 목적 함수와 제약 조건이 모두 선형일 때 사용하는 고전적 기법입니다.
- 문제 형식: min (또는 max) c·x, 단 A·x ≤ b, x ≥ 0
- 선형 구조 덕분에 문제는 볼록 다면체(convex polyhedron) 내의 최적 점을 찾는 문제로 바뀜 → 전역 최적 보장
🔑 대표 알고리즘:
- 심플렉스(Simplex): 꼭짓점을 이동하며 해 찾기 (실무에서 매우 빠름)
- 내부점법(Interior-point method): 다면체 내부에서 이동하며 해 탐색 (다항시간 보장)
🧠 예시: 자원 제약 하에서 공장 생산 계획 수립 → 수익 최대화
💡 Tip: LP는 선형 문제에만 적용되며, 정수 결정 변수나 비선형 목적 함수가 있는 경우는 별도의 기법이 필요합니다.
2.2 경사 기반 최적화 (Gradient-Based Optimization) 📉
**경사 하강법(Gradient Descent)**은 목적 함수가 미분 가능할 때 널리 사용되는 방법입니다. 미분을 이용하여 목적 함수가 줄어드는 방향으로 조금씩 이동합니다.
📌 수식:
x_new = x_current - η ∇f(x_current)
- ∇f: 함수의 기울기 (gradient)
- η: 학습률(learning rate), 얼마나 이동할지
🔄 반복하여 함수 값을 줄이는 방향으로 이동하면 (지역) 최솟값에 수렴하게 됩니다.
🧠 대표적 변형:
- 확률적 경사 하강법(SGD): 데이터 일부만 사용하여 빠르게 진행
- Momentum, Adam: 관성, 적응적 학습률 도입하여 수렴 가속화
- 2차 방법(Newton 등): 헤시안(Hessian)을 사용해 더 정확한 방향 찾기 (계산 부담 큼)
✍ 적용 예: 인공신경망 학습 – 수백만 개의 가중치를 손실 함수를 줄이는 방향으로 조정
2.3 진화 알고리즘 (Evolutionary Algorithms) 🧬
복잡하고 미분 불가능한 문제에 강력한 방법이 바로 진화 기반 최적화입니다. 이는 자연 선택과 유전의 원리를 기반으로 후보 해(population)를 발전시켜 나갑니다.
🎯 대표 알고리즘: 유전 알고리즘(Genetic Algorithm, GA)
🧬 기본 흐름:
- 초기 해 집단 생성 (무작위)
- 선택: 성능 좋은 해 우선 선택
- 교차: 두 해의 일부분 섞어 새로운 해 생성
- 돌연변이: 무작위 변형 삽입하여 다양성 확보
- 대체: 다음 세대로 넘김
🌀 반복하면서 해 집단이 점차 향상됨. 국소 최적에 갇히지 않고 전역 탐색 가능성이 높음.
📚 관련 기법:
- 진화 전략(ES), 유전 프로그래밍(GP)
- 입자 군집 최적화(PSO), 개미 군집 최적화(ACO) 등
⚠️ 단점: 계산량이 크고 수렴 속도는 느림 → 초기 해를 찾은 후 경사법으로 정교화하는 하이브리드 방식도 사용
📌 요약:
- 구조화된 문제: 선형 계획법
- 부드러운 연속 문제: 경사 기반
- 구조가 불명확하거나 비선형적 문제: 진화 알고리즘